Обзор научных трудов К.П. Персидского

Математическая наука в Казахстане за последние десятилетия достигла больших успехов. Математикам нашей республики принадлежит приоритет в разработке ряда вопросов теории дифференциальных уравнений и устойчивости их решений. В этом огромная заслуга безвременно скончавшегося академика Академии наук Казахской ССР, заслуженного деятеля науки КазССР, доктора физико-математических наук, профессора Константина Петровича Персидского.

К. П. Персидский был выдающимся математиком с широким диапазоном научных интересов. Его глубокие исследования, относящиеся к различным разделам математики — теории вероятностей, дифференциальным уравнениям, теории устойчивости движения, интегральным уравнениям, теории функций и функциональному    анализу,    геометрии — логически связаны между собой и представляют существенный вклад в науку. Начиная с первых своих работ, относящихся к теории вероятностей, и кончая работами последних лет жизни по созданию впервые в математической науке теории нелинейных пространств, Константин Петрович выступал как оригинальный, самобытный ученый, которого не удовлетворял установившийся уровень познания законов, он стремился глубже познать механизм их действия и использовать их для создания нового в науке.

Публикуемые Избранные труды Константина Петровича Персидского состоят из двух томов.

В первом томе помещены исследования, относящиеся к теории вероятностей, теории устойчивости решений конечных систем дифференциальных уравнений, и серия работ по различным вопросам теории функций и функционального анализа, геометрии, прикладной математики. Второй том посвящен работам по теории бесконечных систем дифференциальных уравнений, устойчивости их решений и теории нелинейных пространств.

Перейдем к краткому обзору трудов К. П. Персидского.  

Первые работы Константина Петровича были посвящены закону больших чисел и предельным теоремам теории вероятностей. Пробле­мы теории вероятностей интересовали К. П. Персидского на протяжении всего периода его научной деятельности. В 1934 г. за цикл работ по теории вероятностей К. П. Персидский был удостоен звания профессора; всего же по теории вероятностей им опубликовано 14 научных работ.

Ранние работы Константина Петровича посвящены предельным теоремам теории вероятностей. Их появление совпало с периодом качественного скачка и становления советской математической школы теории вероятностей, возглавляемой академиком А. Н. Колмогоровым.

Знакомясь с работами К. П. Персидского того времени, остро чувствуешь, как молодой ученый (26 лет) ищет свой, независимый путь в науке, что становится в последующем важнейшей особенностью его творчества.

Константин Петрович сосредоточивает внимание вокруг жемчужины классической теории вероятностей — закона больших чисел (з.б.ч.). Этот закон привлекал и привлекает внимание многих исследователей. Проблема состоит в том, чтобы установить достаточно широкие условия, при которых последовательность случайных величин удовлетворяла бы з.б.ч., т. е. когда среднеарифметическое случайных величин равносходится по вероятности со среднеарифметическими их математических ожиданий (чебышевская формулировка). Как известно, з. б. ч. является одним из основных предложений теории вероятностей и возник из практических задач, связанных с анализом на статистическую устойчивость результатов наблюдения. 3. б. ч. имеет огромное практическое значение. Известно, например, что большинство схем метода Монте-Карло опирается на з. б. ч. в различных формулировках, а методы Монте-Карло составляют неоценимый конструктивный аппарат исследования сложных систем и явлений посредством вероятностного моделирования на ЭВМ и образуют важный инструмент современной прикладной математики.

Первая работа [2] Константина Петровича "К теореме Маркова" относится к 1929 г. В ней дается некоторое ослабление ограничения известной теоремы Маркова о з.б.ч. Здесь, как и во многих последующих его работах, заметно значительное влияние идей и методов А. А. Маркова. Об этом говорит хотя бы то, что он во многих своих исследованиях использует метод урезания, впервые примененный А. А. Марковым в 1907 г.

1930 и 1931 гг. - это годы интенсивной работы Константина Петровича в избранном направлении. Появляется серия его публикаций, доклады на заседаниях Казанского математического общества ("Уч.зап.Казанского университета", т. 91, кн. 4, Математика, вып. 1; "Известия АН СССР. Отд. мат. и ест.",932, № 5). Здесь К. П. Персидский вводит формулировку з.б.ч. в форме, отличной от чебышевской. Последовательность {x_n } случайных величин (с. в.) удовлетворя­ет з. б. ч., если существует последовательность {с_n} констант такая, что среднеарифметическая с. в. равносходится по вероятности со среднеарифметическими указанных констант.

В частном случае, когда математические ожидания случайных величин x_n  существуют и совпадают с указанными константами, мы получаем формулировку з.б.ч. в форме Чебышева.

К. П. Персидский дает законченное решение проблемы з.б.ч. в новой формулировке для случая, когда последовательность с. в. является независимой. Им даны две теоремы, содержащие необходимые и достаточные условия того, чтобы последовательность независимых случайных величин удовлетворяла з.б.ч. в новой формулировке. Кро­ме того, указаны условия, при которых рассматриваемые константы необходимо совпадают с математическими ожиданиями случайных величин x_n. Эти условия оказались условиями типа Маркова.

Последующие работы [19, 31] по закону больших чисел публи­куются в 1938 г. в ДАН СССР и в 1949 г. в "Ученых записках Казахского государственного университета им. С. М. Кирова". В них обобщены исследования по з.б.ч. на базе понятий равномерной сходимости и в среднем равномерной сходимости последовательности математических ожиданий рассматриваемых случайных величин.

При чтении этих работ поражает глубина аналитических исследований и высокая математическая культура Константина Петровича. Он выступает как большой, сложившийся мастер анализа и исследования свойств бесконечного. Здесь мы с благодарностью должны вспомнить ту школу, которая воспитала Константина Петровича Персидского, — один из крупнейших научных центров страны — Казанский государственный университет им. В. И. Ульянова — Ленина.

При этом уже здесь нетрудно заметить истоки методов, которые в последующем применяли К. П. Персидский и его многочисленные ученики в области бесконечных систем дифференциальных уравнений. Так, широко используемый им метод "урезания" может служить прототипом метода усечения или метода "редукции" при исследова­нии бесконечных систем дифференциальных уравнений. Введенное им понятие равномерной сходимости последовательности математических ожиданий в з.б.ч. для зависимых величин может служить прототипом равномерной устойчивости, а ослабление ограничений на размах абсолютного значения частичных сумм зависимых случайных величин может служить прототипом тех обобщений условий Коши — Липшица, которые он использовал при исследовании бесконечных систем дифференциальных уравнений.

Все это говорит о том, что Константин Петрович умел видеть глубокую аналогию между, казалось бы, совершенно различными математическими концепциями.

Цикл работ К. П. Персидского в области теории вероятностей завершается четырьмя большими научными статьями, посвященными оценке погрешности запаса месторождений [49, 52, 60, 63]. Они являются непосредственным следствием исследований по закону больших чисел. В них используются результаты и опыт предшествующих разработок.

Рассматривается следующая модель.

Случайная величина x представляет количество полезного ископаемого (в некоторых единицах) в различных точках поверхности месторождений. Значения случайных величин при этом считаются независимыми. Величина запаса определяется как некоторая функция математического ожидания случайной величины. Требуется оценить модуль разности между выборочной средней и математическим ожиданием самой случайной величины.

Известная оценка из теории выборок не удовлетворяет Константина Петровича. Он стремится получить оценки более высокой степени точности. Используя теорему Ляпунова, неравенство Чебышева, получает тонкие оценки погрешности в тех случаях, когда выборочная дисперсия оказывается достаточно близкой к истинной.

Вся творческая жизнь Константина Петровича отмечена глубоким интересом к прикладным задачам. В данный том включены так­же работы по теории функций и функциональному анализу, геометрии и статьи, посвященные некоторым прикладным вопросам, сопут­ствующим основному творческому поиску автора.

В работе [1] приводятся достаточные признаки существования решений систем интегральных уравнений (Вольтерра, Фредгольма). Она восхищает филигранностью и высокой техникой математических преобразований.

В работе [4] приведена одна оценка для модуля корня голоморфной функции.

В работе [40] анализируются вопросы построения моделей прост­ранства Лобачевского в трехмерном пространстве Евклида.

В работе [41] дается построение интеграла Лебега для функций, заданных на измеримых множествах n-мерного евклидового пространства со значениями в полном линейном нормированном пространстве.

В работе [45] вводятся понятия дуги в нормированных пространствах, угла между элементами и способы их измерения, понятия кру­чения вектора, площади. Обращается внимание на то, что в общем случае для линейных нормированных пространств не будет справедливой аксиома о конгруентности треугольников, из-за чего в каждой плоскости нормированного пространства для измерения площадей плоских фигур приходится вводить свою единицу измерения. Этот факт составляет одну из важнейших специфических особенностей теории измерения геометрических фигур в линейных нормированных пространствах.

В работе [46] метод Лобачевского приближенного вычисления корней алгебраического уравнения распространяется на случай трансцендентных уравнений, описываемых голоморфными функ­циями.

В работе [47] указывается на определенную ценность для процесса познания использования биективных отображений множеств на множества, индуцирующие свойства элементов множеств определений на элементы множества значений.

В работе [54] приведены оценки для производной нормы функции x(t) со значениями в банаховом пространстве.

В работе [61] приведены критерии вложенности сфер в пространстве Банаха и вытекающие отсюда следствия: имеет место сходимость центров и радиуса бесконечной последовательности вложенных сфер, пересечение замкнутых вложенных сфер есть замкнутая сфера и т. п.

Работы К. П. Персидского по теории конечных и бесконечных систем дифференциальных уравнений и устойчивости их решений можно разбить (условно) на следующие три группы:

1)     исследование устойчивости решений конечных систем дифференциальных уравнений;

2)     развитие общей теории бесконечных    систем дифференциальных уравнений и дифференциальных уравнений в линейных нормированных пространствах и исследование устойчивости их решений;

3)     создание некоторых нелинейных пространств и рассмотрениe вопросов анализа и дифференциальных уравнений в таких пространствах.

Хронологически творческую биографию К. П. Персидского можно (также условно) разбить на два периода: казанский (до 1940 г.) и ка­захстанский (1940—1970 гг.).

Работы по первому из указанных выше трех направлений велись в оба периода, а по второму и третьему — целиком во второй период.

Исследования по теории устойчивости Константин Петрович начал как активный участник организованного Н. Г. Четаевым при Ка­занском университете научного семинара по теории устойчивости движения. В трудах членов этого семинара — Н. Г. Четаева, К. П. Персидского, Г. В. Каменкова и И. Г. Малкина — получили дальнейшее развитие фундаментальные исследования по теории устойчивости выдающегося русского математика и механика академика А. М. Ляпунова.

Основными проблемами, интересовавшими участников семинара, были: обращение основной теоремы Ляпунова об устойчивости, устойчивость по первому приближению; получение более общих теорем о неустойчивости; теория характеристичных чисел и исследование критических случаев. В решении каждой из этих проблем К. П. Персидский находил совершенно новые, оригинальные пути, а полученные им результаты послужили основой для дальнейших творческих поисков.

Уже в первой работе [8] по теории устойчивости движения, опубликованной в 1931 г., Константином Петровичем были приведены оценки решений дифференциальных уравнений, полученные с помощью форм т-го порядка; для доказательства некоторых новых теорем второго метода Ляпунова используются функции Ляпунова вида u=j(t)u; впервые дана постановка задачи устойчивости на конечном промежутке времени и указаны пути решения этой задачи методом функций Ляпунова, в частности, указаны оценки области начальных возмущений и оценки величины промежутка времени, на котором решения системы остаются в некоторой данной области; рассмотрены некоторые вопросы устойчивости по первому приближению и впервые приведено замечание о том, что в случае асимптотической устойчивости невозмущенного движения интегральные линии системы могут стремиться к нулю "неравномерно".

Многие идеи этой статьи получили развитие в последующих работах К. П. Персидского, посвященных исследованию устойчивости конечных систем дифференциальных уравнений.

Так, например, в работах [10, 12], опубликованных в 1933 г., К. П. Персидским были впервые введены понятия равномерной устойчивости и равномерной асимптотической устойчивости, ставшие позднее классическими понятиями теории устойчивости наравне с основ­ными определениями, введенными самим А. М. Ляпуновым; получены необходимые и достаточные условия равномерной устойчивости по первому приближению; показано, что в случае, когда уравнения первого приближения удовлетворяют условиям теоремы А. М. Ляпунова об асимптотической устойчивости, будет иметь место и равномерная асимптотическая устойчивость по первому приближению; сделано замечание [12] о том, что если правые части системы уравнений невозмущенного движения не зависят от времени t, то устойчивое решение такой системы будет и равномерно устойчивым; показано [10], что условие положительности характеристичных чисел не является необходимым условием устойчивости по первому приближению. Приведено несколько достаточных условий устойчивости по первому приближению, в частности, получен один критерий равномерной устойчивости в критическом случае (п—1) нулевых корней.

В работе [14] (1934 г.) рассмотрен вопрос о периодических возмущениях, а в работе [15] приведен новый подход к решению проблемы теории устойчивости.

Исключительно важное значение в развитии теории устойчивости движения имело решение К. П. Персидским [8], в общем виде, вопроса обращения теоремы Ляпунова об устойчивости, показавшее логическую завершенность и универсальность второго метода Ляпунова и положившее начало многочисленным исследованиям, посвященным проблеме существования функций Ляпунова. Отметим, что полученная при этом Константином Петровичем теорема носит и конструктивный характер.

Особо следует отметить фундаментальную работу [17, 20] "К теории устойчивости интегралов системы дифференциальных уравнений", в которой К. П. Персидский подводит итоги исследований по теории устойчивости движения, выполненные в начале 30-х годов. В ней же охвачено и основное содержание работ [10, 12, 13, 15, 18], поэтому в данном томе они не публикуются.

В работе [17] дано обобщение одной теоремы А. М. Ляпунова об устойчивости по первому приближению в случае, когда система первого приближения является правильной. Далее показано, что необходимыми и достаточными условиями равномерной устойчивости по первому приближению является существование для решений системы уравнений первого приближения оценки вида

||x(t, t₀,,x₀)||£ Bexp [- a(t-t₀)],

где a>0 и B³1 - некоторые постоянные. Это неравенство, назван­ное впоследствии в специальной литературе свойством «экспоненци­альной устойчивости», играет и в настоящее время весьма важную роль во многих разделах общей теории дифференциальных уравнений. Показано, что в случае выполнения для системы первого приближения условий теоремы А. М. Ляпунова об асимптотической устойчивости неравенство (1) обязательно будет иметь место. Затем подробно исследуется критический случай (п—1) нулевых корней.

В работе [20] К. П. Персидским впервые введено понятие "функции со слабой вариацией" и проведены исследования по устойчивости решений линейных систем дифференциальных уравнений, коэффициенты которых суть функции со слабой вариацией. Приведены оценки характеристичных чисел решений указанной выше системы дифференциальных уравнений и введено понятие устойчивости характеристичных чисел. Рассмотрен вопрос обращения теоремы Ляпунова об устойчивости.

Глубокие исследования по теории устойчивости конечных систем дифференциальных уравнений были выполнены К. П. Персидским в 1943—1944гг. Результаты этих исследований вошли в его докторскую диссертацию [22] "К теории устойчивости решений дифференциальных уравнений", которая была им защищена в МГУ в 1946 г.

Основными вопросами, рассмотренными в диссертации, были: развитие второго метода Ляпунова; устойчивость по первому приближению; характеристичные числа линейных систем дифференциальных уравнений, коэффициенты которых являются функциями со слабой вариацией; некоторые свойства правильных систем линейных дифференциальных уравнений.

Резюме докторской диссертации приведено в работе   [23].

Из результатов, относящихся к первой группе вопросов, рассмотренных в диссертации, особенно важное значение для развития второго метода Ляпунова имели теоремы К. П. Персидского о неустойчивости, основанные на введенном им понятии "сектора".

В частности, им была доказана следующая теорема, являющаяся и сейчас одной из наиболее общих теорем о неустойчивости [25].

Пусть система уравнений возмущенного движения такова, что существует сектор w, в котором некоторая функция u и ее полная про­изводная u¢ удовлетворяют условиям:

1)    внутри и на границе сектора w функция v ограничена;

2)  во всякой внутренней точке области w функция u’³h(t,u)³0,
где h(t,u)  не убывает по u и и при любом a>0

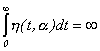        (2)

Тогда нулевое решение рассматриваемой системы уравнений неустойчиво.

Исследования по общей теории и теории устойчивости решений конечных систем дифференциальных уравнений проводились К. П. Персидским и в послевоенные годы, когда он разрабатывал теорию бесконечных систем дифференциальных уравнений и дифференциальных уравнений в линейных нормированных и введенных им в рассмотрение нелинейных пространств L и w. Среди работ, относящихся к этому кругу вопросов, особо нужно отметить статьи [24, 29, 59], посвященные развитию теории характеристичных чисел и вопросу построения обобщенных решений системы обыкновенных дифференциальных уравнений при самых общих предположениях относительно ее правых частей.

Заметим, что в работе [24] получила дальнейшее развитие сфор­мулированная К. П. Персидским проблема устойчивости характеристичных чисел. В ней приведены критерии такой устойчивости, позво­ляющие в некоторых случаях значительно облегчить отыскание самих характеристичных чисел. Для правильных систем установлена зависимость между характеристичными числами данной системы и присоединенной системы дифференциальных уравнений. Показано, что характеристичные числа линейной системы, коэффициенты которой являются функциями со слабой вариацией, имеют много общего с характеристичными числами линейных систем с постоянными коэффициентами. Изучены некоторые свойства характеристичных чисел систем дифференциальных уравнений с периодическими коэффициентами.

Начиная с конца 40-х годов К. П. Персидский обращается к систематическому качественному исследованию бесконечномерных дифференциальных систем. Как отмечали в те годы ведущие советские специалисты по дифференциальным уравнениям и теории устойчивости движения, "... в этой совершенно не исследованной ранее области Константину Петровичу принадлежат как постановка задачи, так и установление основных теорем".

В серии статей [26, 28, 30, 33, 35—37, 39], опубликованных в 1948—1951 гг., К. П. Персидский изложил полученные им фундаментальные результаты по следующим ветвям указанного направления: общая теория счетных и бесконечных (произвольной мощности) систем дифференциальных уравнений; счетные системы линейных дифференциальных уравнений и теория характеристичных чисел; ус­тойчивость решений счетных систем дифференциальных уравнений; счетные системы уравнений в частных производных; дифференциальные уравнения в банаховых пространствах и устойчивость их решений; некоторые критические случаи устойчивости в счетных системах.

Приведем кратко некоторые из основных результатов.

Результаты первых исследований, выполненных Константином Петровичем в 1947 г., были опубликованы в 1948 г. в двух больших его работах [26, 28]. Основным объектом исследований в них была система вида

            (3)

названная автором счетной системой дифференциальных уравнений, в которой искомые функции (вещественные или комплексные) от ве­щественной независимой переменной t подчинены требованию ||x||=sup{|x₁|, |x₂|,…}<¥.

Предполагая, что в области

t ³ 0, |x_s| £ R ( s = 1, 2,…).         (4)

где R >0 — некоторая (конечная) постоянная, функции w_s(t, x₁, x₂, . . .) непрерывны по t, удовлетворяют условию Липшица по х₁, х₂, . . . , w_s(t, 0,0, . . .) = 0, s = 1, 2, 3... и при любых конечных значениях х₁, х₂, . . . и  t ³ 0 выполняется условие |w_s(t, x₁, x₂,, . . .)| £ b (t), где b (t) — некоторая непрерывная функция при t ³ 0, был рассмотрен достаточно широкий круг вопросов. Было доказано существование у системы (3) единственного равностепенно-непрерывного решения (тем самым и ограниченного), проходящего через заданную внутреннюю точку (t₀, x₁⁰, x₂⁰,…) области (4), которое непрерывно зависит от своих начальных значений; дан способ построения искомого решения посредством использования некоторой вспомогательной (так называемой укороченной) системы дифференциальных уравнений; для случая, когда функции w_s линейны относительно х₁, х₂, ..., указано условие, при выполнении которого линейная комбинация от счетного множества решений системы также является ее решением; приведена оценка снизу и сверху нормы решения линейной системы. Была дана постановка задачи об устойчивости нулевого решения х₁ = x₂ =…= 0 системы (3), показана применимость второго метода Ляпунова для исследования устойчивости, доказана обратимость первой теоремы Ляпунова, установлено достаточное условие равномерной и асимптотической устойчивости по первому приближению. Последний результат вскоре был расширен и в работе [33], выполненной в конце 1949 г., дан общий критерий равномерной устойчивости по первому приближению.

Называя   характеристичным    числом    решения    x_j = х_j (t)(j = 1, 2, ...) линейной системы

   (5)

характеристичное число его нормы, а спектром характеристичных чисел - совокупность характеристичных чисел всех решений системы (5), отличных от нулевого решения, Константин Петрович в работах [30, 36] доказал ряд важнейших теорем о характеристичных числах, о спектре характеристичных чисел (в частности, было показано, что этот спектр может быть конечным, счетным, мощности континиума) и спектральных признаках устойчивости.

Указанные работы явились основополагающими для более широкой разработки теории счетных систем дифференциальных уравнений и устойчивости их решений.

Глубину и значительность научных достижений К. П. Персидского по теории бесконечных систем дифференциальных уравнений наиболее ярко характеризует выполненное им в 1949 г. исследование [35], которое оказало большое влияние на дальнейшее развитие этой теории. Ввиду фундаментальной важности этой работы приведем, хотя бы кратко, ее содержание.

Известно, что при исследовании критических случаев в теории устойчивости для конечных систем дифференциальных уравнений А. М. Ляпунов пользовался некоторыми преобразованиями, позволяющими упростить вид изучаемых уравнений. Многие продолжатели Ляпунова также широко пользовались подобного рода преобразованиями. Такие преобразования приводят к необходимости рассматривать систему уравнений в частных производных специального вида. Применительно к нуждам теории счетных систем дифференциальных уравнений Константин Петрович, обобщая идеи А.М.Ляпунова, ввел в рассмотрение систему уравнений

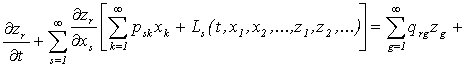
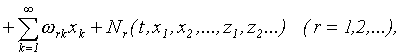  (6)

где L_s  и N_r — вещественные непрерывные функции в вещественной области :

t³0,  |x_s| £ R,   | z_s | £ R (s,r=1, 2,. . .),

а p_sk, q_rg, w_rk суть вещественные и непрерывные функции переменной t³0, причем L_s и N, обращаются в нули при x₁=x₂=…=z₁=z₂= …=0. Подчиняя указанные функции некоторым условиям, вытекающим из самого характера рассматриваемой задачи, автор показал существование у системы (6) единственного ограниченного решения, т. е. решения z_r= z_r (t, х₁, х₂, . . . ) (r = 1, 2, ... ), удовлетворяющего требованию

| zr(t, х1, х2,…)|£g<R(r=1,2,..)

при всех значениях t³0 и x_s таких, что | х_s |£ p£ R(s = 1, 2, ...). Такое решение и определяет искомое преобразование.

В этом же исследовании, основанном на использовании весьма тонких методов теории дифференциальных и интегральных уравнений, был разработан метод, который впоследствии успешно применялся при рассмотрении многих важных задач теории дифференциальных уравнений. Появление ее позволило приступить к изучению критических случаев счетных систем и дифференциальных уравнений в нормированных пространствах, дало возможность развернуть исследования значительного круга вопросов общей теории счетных систем уравнений в частных производных первого порядка и т.д.

В работе [39] была рассмотрена система вида

               (7)

Подчиняя определенным условиям функции, входящие в правые части системы, а также решения линейных однородных систем

     Константин Петрович относительно нулевого решения x₁= x₂=…= y_l = y₂=…=0 системы (7) доказал ряд теорем об условной устойчивости (при численно достаточно малых начальных значениях величин х₁, х₂, . . . ), неустойчивости и равностепенно асимптотической устойчивости. При этом, используя решение системы вида (6), он под­вергал исследуемую систему (7) преобразованию, инвариантному по отношению к устойчивости.

В ряде своих исследований, начиная с работы [35], Константин Петрович в соответствии с характером рассматриваемой задачи под­чинял функции w_s в системах вида (3), L_s и N_r в системе (6) и т. д. некоторому специальному условию, называя его «усиленным условием Коши». Применительно к функциям w_s в системе (3) оно имеет следующий вид:

    (8)

где a(t) — непрерывная функция от t, Dx = sup{|x'_m —  x'¢_m|, |х'_т+1 - х¢'_т+1|,

|х'_т+2 - х¢'_т+2|,…}, e_s(m)®0 при m®¥ и фиксированном s.

При наличии этого условия и выполнении ранее приведенных условий относительно функций w_s в области (4) решение x_s=j_s(t, t₀, x₁⁰, x₂⁰, …) (s=1, 2…) системы (3), проходящее через точку (t₀, x₁⁰, x₂⁰, …), можно построить методом так называемой укороченной системы, а именно, если и_вт=j_sm(t), s=l, 2, ... есть решение системы

удовлетворяющее условию  j_sm(t₀)=x⁰_s, то  x_s=j_s(t, t₀, x₁⁰, x₂⁰, …)=limj_sm(t) (s=1, 2…).

Существует много задач, в которых соответствующие функции подчиняются условию вида (8).

Условие (8) и метод укороченных систем были использованы учениками К. П. Персидского для установления основных положений о голоморфных решениях счетных систем дифференциальных уравнений. Это же условие или его видоизменения были широко использованы в ряде других исследований: в уравнениях в частных производных со счетным множеством независимых переменных, в доказательстве дифференцируемости решений счетных систем вида (3) по начальным значениям и распространении случая Каратеодори на счетные системы, в исследовании устойчивости решения задачи Коши для счетных систем уравнений в частных производных и т. д.

Результаты, полученные К. П. Персидским в упомянутых выше работах [26, 28, 30, 33, 36] по счетным системам дифференциальных уравнений, в дальнейшем были им несколько переработаны и в систе­матизированном виде изложены в трех его работах [50, 53, 56], которые будут помещены во втором томе Избранных трудов.

Исходя из того, что многие задачи, связанные с изучением устойчивости движения материальных систем с бесконечным множеством
степеней свободы, приводят к необходимости рассмотрения бесконечных систем уравнений произвольной мощности, К. П. Персидским
рассматривались системы вида

  (9)

и дифференциальные уравнения в нормированных пространствах. Первые результаты в этом направлении были получены им в 1949-1950 гг. и опубликованы в работе [37].

В системе вида (9) предполагается, что индексы a иb пробегают некоторое множество s. Система (3) является одним из частных случаев системы (9), когда s— счетное множество. Для случая s= [0, 1] система вида (9) была раньше рассмотрена А. Н. Тихоновым и дано доказательство теоремы существования решения (см. В. В. Немыцкии. Метод неподвижных точек в анализе. УМН, 1936, в. 2). К. П. Персидский разработал вопросы общей теории и устойчивости решений таких систем для случая множества а произвольной мощности.

Совокупность величин ..., х_а,... в системе (9) можно рассматривать как координаты точки х = (..., х_а,. . .) бесконечномерного про­странства, само пространство — как совокупность таких точек; такое пространство обращается в линейное, если положить

(…, x_a ,…)+(…,y_a, …)=(…, x_a+y_a,…), c(…, x_a,…)=(…, cx_a,…),

где с — любое число.

Из этого пространства можно выделить нормированную часть, для чего достаточно, например, рассмотреть лишь совокупность всех тех точек х = (.. ., х_a,...), координаты которых удовлетворяют условию sup{..., | x_а |,...}<¥, и положить||x||=sup{..., | x_a|,...}. Тогда систему уравнений (9) можно записать в векторной форме в виде одного уравнения             (10)

так что f_b  (t,. . . , x_a,...) является b-й составляющей вектора f(t, х).

Система вида (9) может быть рассмотрена в более общем смысле, если полагать, что каждая из искомых величин дгр является элементом некоторого полного линейного нормированного пространства Мр, которому принадлежат также и значения функций

f_b(t,…,x_a,…)

Такому подходу к теории систем указанного вида посвящены работы [43,62].

В связи с рассмотрением дифференциальных уравнений в полных линейных нормированных пространствах в работах [45, 54, 41, 48] были изучены также некоторые вопросы геометрии и теории абстрактных функций в таких пространствах.

Значительное число исследований Константин Петрович посвятил решению задачи Коши и построению ограниченного решения некоторого специального класса функциональных уравнений. Он установил, что изучение ряда вопросов устойчивости решений дифференциальных уравнений в нормированных пространствах приводит к рассмотрению в этих пространствах функциональных уравнений вида

    (11)

и

 (12)

где t — вещественная переменная ; х — переменная, область изменения которой принадлежит произвольно заданному полному линейному нормированному пространству М; v(t, х) — искомая функция от t и х с областью значений в некотором произвольно заданном полном линейном нормированном пространстве N, а f и j — заданные функ­ции своих аргументов, области значений которых принадлежат соот­ветственно пространствам М и N.

Уравнение (11), являющееся частным случаем уравнения (12), встречается, например, при построении функции Ляпунова v = v(t, х) для дифференциального уравнения

в предположении,    что ее полная   производная v¢  имеет   заданное значение j(t, х).

Если точка v = v(. . . , v_a, . . . ) пространства N определяется конечным или бесконечным множеством координат v_a , где v_a изменяется в некотором полном линейном нормированном пространстве А _а , а a принимает всевозможные значения из некоторого множества s ин­дексов, то уравнение (12) обращается в бесконечную систему урав­нений

 (13)

где b принимает всевозможные значения из s. Если пространства N и М счетно-мерные, то уравнение (12) при выполнении некоторых дополнительных условий относительно функций f и j_b обращается в счетную систему вида

частным случаем которой является ранее рассмотренная система (6).

В своем докладе [44], представленном III Всесоюзному математическому съезду в 1956 г., Константин Петрович дал решение задачи Коши для уравнений (11) и (12), а позднее, в работе [64], подобную задачу он решил для системы вида (13) при более общих предположениях, что искомые функции v_а являются элементами соответствующих полных линейных нормированных пространств N_a .

В последние 5 — 6 лет жизни творческая деятельность К. П. Персидского протекала также весьма плодотворно. Основное его внимание в эти годы было направлено на создание нового класса пространств, названных им нелинейными, и разработку основ теории дифференциальных уравнений (и устойчивости их решений), в которых искомые функции имели бы значения, принадлежащие таким пространствам. Первые свои результаты в этом направлении он изложил в работе [58] . Введенное им здесь так называемое пространство L характеризуется тем, что не предполагается свойство коммутативности в операции сложения элементов. Аксиоматически определив это пространство как нормированное и полное, К. П. Персидский вводит в нем понятия производной и интеграла от функции вещественной переменной, доказы­вается теорема существования и единственности решения дифференциального уравнения. Несколько    позднее в работе [66]  было    дано решение задачи Коши для функционального уравнения вида

и системы (бесконечной) таких уравнений. При этом t — вещественная независимая переменная, х и v — элементы соответственно пространств М и N типа L, a f(t, х, v) и j(t, х, v) — заданные функции в области 0£t£b, ||х||_м £ R, ||v|| _N £ R и удовлетворяющие в этой области определенным условиям, заключающимся в непрерывности по t и выполнении условия, аналогичного условию Липшица по х и v.

В 1967 г. Константин Петрович в работе [65] ввел новое нелинейное пространство, которое обозначил через w. Это пространство также было определено аксиоматически, причем в операции сложения элементов не предполагаются выполненными свойства коммутативности и ассоциативности. Пространство предполагается нормированным и полным. Имея в виду дальнейшее использование этого пространства (как и в случае пространства L), предполагается, что для любого нату­рального п выполняется неравенство

,

где a_k — числа (вещественные или комплексные), х₁, . . . , х_п ; у₁, у₂, . . ., …,y_n cyть элементы из w, A = A(v)³ l некоторая непрерывная возрастающая функция при v³0, причем за величину v можно взять любое число, удовлетворяющее условию

Заметим, что в случае пространства Банаха, как известно, А = 1.

В качестве примера пространства w указывается пространство Лобачевского, а именно : если в пространстве Лобачевского умножение векторов на вещественные числа понимать в обычном смысле, то можно так ввести операцию сложения векторов (с общей начальной точкой), что пространство Лобачевского будет обладать свойствами пространства w.

В той же работе были введены понятия производной и интеграла от функции вещественной переменной и установлены их свойства. Если j(t)Îw есть функция, заданная на сегменте [а, b], то производ­ной ее в точке t называется такой элемент yÎw, что

Было дано доказательство теоремы существования и единственности решения дифференциального уравнения x' = f(t, х) с искомой функцией x = x(t)Îw. В последующих работах [70, 71] была доказа­на применимость метода Эйлера для приближенного интегрирования дифференциального уравнения, введено понятие ряда Тейлора для функции f(t)Îw  от вещественной переменной t.

В заключение отметим, что к разработке широкой научной тема­тики Константин Петрович Персидский привлек большую группу математиков и создал в Казахстане математическую школу по диффе­ренциальным уравнениям и теории устойчивости движения, заслужен­но пользующуюся известностью в нашей стране и за ее пределами. Результаты многолетних исследований дали богатый материал для соз­дания ряда специальных курсов (теория устойчивости для конечных систем, счетные системы дифференциальных уравнений и дифференциальные уравнения в нормированных пространствах и устойчивость их решений, абстрактные голоморфные функции и их приложения к дифференциальным уравнениям, нелинейные пространства) и спецсеминаров (теория критических случаев и др.)" которые в течение многих лет читались и читаются на механико-математическом факультете КазГУ и позволяют готовить математиков по достаточно широкой программе в области дифференциальных уравнений.

В последние годы жизни К. П. Персидский работал над созданием монографии по дифференциальным уравнениям в нормированных пространствах и устойчивости их решений. Состояние здоровья не позволило ему закончить эту работу. В конце второго тома данного издания публикуются отработанные им пять глав рукописи.

Т. И. АМАНОВ, В. М. АМЕРБАЕВ,

 Г. Н. БАГАУТДИНОВ, О. А. ЖАУТЫКОВ,

С. К. ПЕРСИДСКИЙ.